Binary search | Tìm kiếm nhị phân

Mô tả

Để triển khai thực hiện một thuật toán nào đó, chúng ta cần phải tìm hiểu một cách chi tiết:

• Nguyên nhân của vấn đề là gì
• Kết quả xử lý
• Biến nào nên được tạo? Giá trị ban đầu của chúng là gì?
• Các bước trung gian nào cần được thực hiện để tính các giác trị khác và cuối cùng để tính đầu ra.
• Liệu các bước thực hiện có sự lặp lại có thể đơn giản hóa bằng việc sử dụng vòng lặp để tính.

Mục tiêu của tìm binary search là theo rút ngắn phạm vi dự đoán một cách hợp lý nhất. Tôi lấy 1 ví dụ, giả sử như tôi có một số tiền chẵn trong khoảng 100 đồng, bạn đoán nó là 30 đồng, tôi nói con số này cao hơn, bạn lại đoán nó là 85 đồng, tôi lại bảo ít hơn số này, do đó lần đoán tiếp theo bạn sẽ thu hẹp phạm vi lại trong khoảng 31-84 đồng. Trong mỗi lần đoán tiếp theo, bạn lại chia khoảng đoán thành 2 phần bằng nhau và lấy điểm giữa để chọn kết quả, ví dụ như (31+84)/2, vì nó là số chẵn nên bạn chọn 57 làm kết quả, nếu tôi nói số này còn cao, thì bạn sẽ coi như khoảng từ 57-84 không có giá trị trong lần đoán tiếp theo và chỉ đoán trong khoảng 31-56 thôi. Và cứ tiếp tục vận dụng cách trên cho đến khi bạn tìm ra kết quả.

Dựa trên ví dụ trên, ta có thể phân tích tiếp, chọn một số min và max là 2 số đầu và cuối trong khoảng đoán, số liệu đầu vào lớn nhất là một số n, ta có thể giả định số nhỏ nhất là 0 và nó có thể điều chỉnh ở lần đoán tiếp theo. Và các bước để thực hiện việc tìm kết quả như cách ở trên tuần tự ta có:

• min = 0, max = n
• Lấy số trung bình làm kết quả
• Nếu nó đúng, tức là kết quả đã tìm ra. Việc tìm kiếm kết thúc
• Nếu số đoán thấp quá, thì min sẽ bằng số tiếp theo cao hơn của kết quả
• Nếu số đoán cao quá, thì max sẽ bằng số tiếp theo nhỏ hơn của kết quả
• Quay lại bước 2.

Triển khai thuật toán

Dựa trên các bước, lấy ví dụ để tìm index của một số bất kỳ trong dãy số nguyên tố, ta có thể triển khai binary search như sau:

• Đặt min, max là hai vị trí đầu cuối của array, count là số lần đoán để tìm kết quả để ta biết được cần phải đếm bao nhiêu lần để tìm thấy (hoặc không tìm thấy kết quả, guessedIndex là vị trí tìm ra kết quả
• Sử dụng vòng lặp while với giới hạn min nhỏ hơn hoặc bằng max. Sau mỗi lần đếm ta cộng thêm 1
• Vị trí của lần đoán bằng giá trị trung bình cộng của max và min lấy theo số nhỏ hơn
• Nếu giá trị cần tìm bằng giá trị tại vị trí đoán, tức là ta tìm thấy kết quả
• Nếu giá trị cần tìm nhỏ hơn hoặc bằng giá trị tại vị trí của lần đoán thì ta lại đặt max bằng vị trí đã đoán trừ 1 và hàm sẽ tiếp tục lặp để tìm theo đó
• Ngược lại (tức là giá trị tìm lớn hơn giá trị tại vị trí của lần đoán) thì min sẽ lớn hơn vị trí đó cộng 1, hàm tiếp tục lặp để tìm.

function binarySearch(targetValue, array) {
  let min = 0;
  let max = array.length - 1;
  let count = 0;
  let guessedIndex;

  while (min <= max) {
    count++;
    guessedIndex = Math.floor((max + min) / 2);

    if (array[guessedIndex] === targetValue) {
      return `Total count is ${count} times, and result is at ${guessedIndex}`;
    } else if (targetValue <= array[guessedIndex]) {
      max = guessedIndex - 1;
    } else {
      min = guessedIndex + 1;
    }
  }

  return `Total count is ${count} times, and result is not found`;
}

const primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97];

const result = binarySearch(73, primes);
console.log(result);

Đo lường hiệu suất

Bạn đã biết rằng đối với linear search cho n phần tử có khả năng phải thực hiện đến n lần tìm kiếm, và bạn có thể suy đoán được là với binary search thì số lần tìm sẽ ít hơn so với linear search, và trường hợp xấu nhất của cả 2 thuật toán khác nhau khi kích cỡ của array tăng lên.

Chìa khóa của thuật toán binary search là sau mỗi lượt thực hiện phép tìm sai, thì khoảng tìm sẽ thu hẹp lại bằng một nửa lúc ban đầu. Ví dụ như ban đầu nó là 50 đơn vị thì sau 1 lần đoán nó chỉ còn 25 đơn vị, cứ tiếp tục như vậy, nó sẽ thu hẹp lại 1 nửa sau mỗi lần đoán sai.

Giả sử như trong một dãy 8 đơn vị, sau mỗi lần đoán nó là 4, rồi 2, rồi 1, khi chỉ còn 1 đơn vị như vậy mà kết quả không được tìm thấy, nghĩa là hoàn tất việc tìm kiếm. Vậy với một dãy gồm 8 đơn vị thì bạn phải mất ít nhất 4 lần tìm. Tương tự, với 16 đơn vị thì ta sẽ có 5 lần tìm. Đó, bạn đã rõ cơ chế của nó, cứ mỗi lần gấp đôi kích thước, thì ta lại tăng 1 lần tìm. Nếu đặt số lần đoán nhiều nhất của array n là m, nếu kích thước của array là 2n, thì lần tìm đầu tiên của nó là n, số lần đoán nhiều nhất của nó là m+1.

Một cách tổng quan, ta có thể tính hiệu suất của thuật toán với array có kích thước n là: số thời gian chia đôi liên tục bắt đầu từ n, cho đến khi ta có giá trị bằng 1, cộng với lần tìm. Nghe có vẻ hơi khó diễn đạt nhưng dùng toán ta có thể sử dụng hàm logarit cơ số 2 log₂n, ta có thể nhìn vào bảng sau để dễ hình dung.

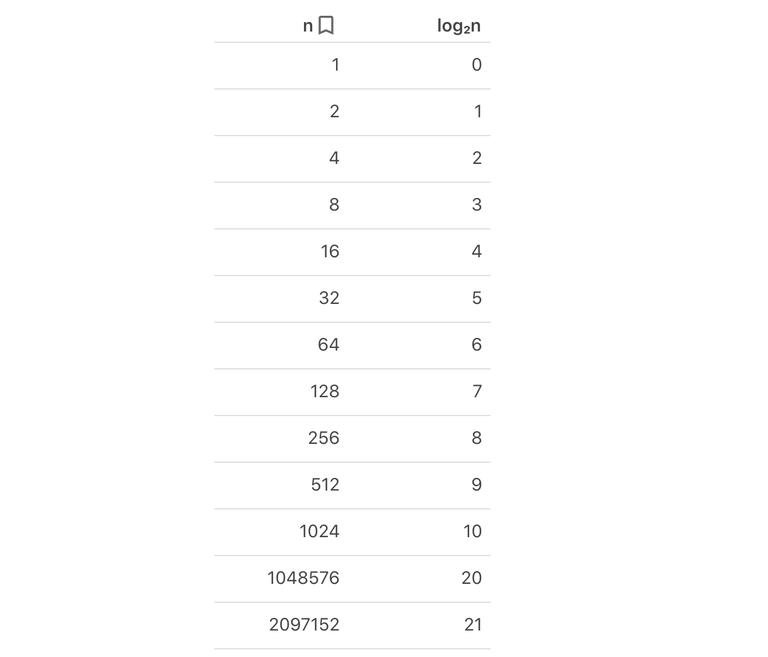
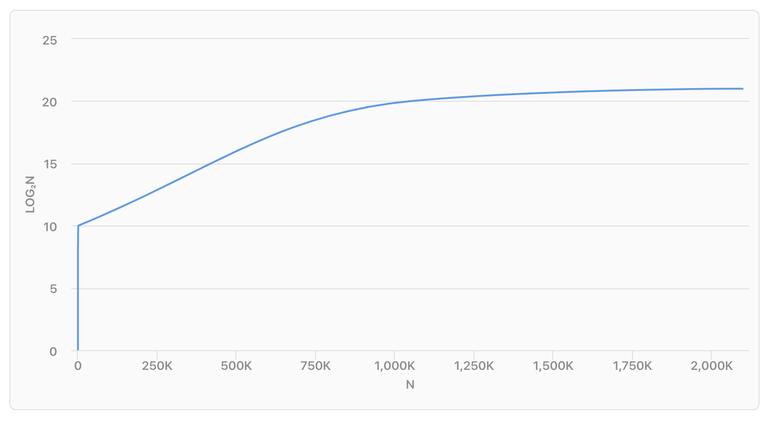
Theo đồ thị ta thấy logarit tăng trưởng rất chậm, như ta đã biết, logarit là đối nghịch của cấp số mũ (tốc độ tăng trưởng rất nhanh), theo như toán học thì nếu log₂n=x thì n= 2ˣ . Ví dụ log₂128=7 thì 2⁷=128.

Nhờ hàm logarit mà việc tính hiệu suất của binary search trở nên dễ dàng hơn với một array khi n là lũy thừa của 2, nếu n=128 thì binary search cần log₂128 + 1 lần đoán.

Điều gì sẽ xảy ra nếu n không phải là số lũy thừa của 2? Lúc này ta có thể lấy số lũy thừa của 2 là số thấp hơn gần nó nhất. Ví dụ cho 1 array kích cỡ 1000, số lũy thừa của 2 gần nhất là 512, tức là 2⁹, do đó ta có thể tính được log₂1000 là một số lớn hơn 9 và thấp hơn 10 (chính xác là 9.97). Cộng thêm 1 ta có 10.97, với trường hợp kết quả là số thập phân thì ta làm tròn theo số thấp hơn để làm kết quả cho số lần đoán.

Ta có thể so sánh hiệu suất với linear search để thấy sự khác biệt

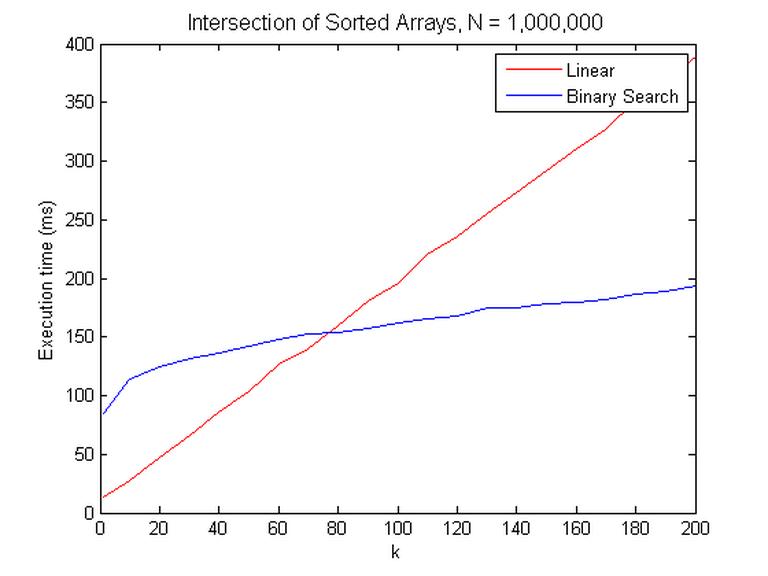
Kết luận

Tôi chắc rằng bạn đã dùng thuật tìm kiếm kiểu này nhiều lần mà không biết rằng mình đang dùng thuật tìm kiếm tương tự như tìm kiếm nhị phân, ví dụ như tra từ điển, thay vì các bạn lần từng từ một từ đầu đến cuối, bạn sẽ lật ra đâu đó trong khoảng ước lượng của cuốn từ điển, rồi thu hẹp phạm vi nó lại, cho đến khi tìm đến trang đích có chứa từ đó.

Khi dữ liệu đủ lớn và được sắp xếp, bạn có thể sử dụng binary search để tiết kiệm thời gian xử lý, tiết kiệm bộ nhớ. Trong trường hợp dữ liệu của bạn thay đổi vị trí sắp xếp thường xuyên (thêm vào, bớt đi), bạn không nên áp dụng thuật toán này.