Selection sort | Sắp xếp chọn lựa

Ví dụ, khi chơi tiến lên, chúng ta hay tìm cách sắp bài của mình theo một trình tự nào đó, việc này giúp chúng ta dễ dàng chọn quân bài một cách hợp lý, bạn nghĩ là trong các lá bài của mình có “sảnh”, để sắp được “sảnh” bạn sẽ tuần tự làm theo các bước sau:

• Tìm lá bài nhỏ nhất trong toàn bộ lá bài, xếp nó sang vị trí đầu tiên.
• Tìm lá bài nhỏ thứ hai, xếp nó vào vị trí tiếp theo
• Tìm lá bài thứ 3, xếp nó ở vị trí tiếp theo lá bài thứ 2
• Tiếp tục tuần tự cho đến khi đủ bộ “sảnh”

Tên gọi “selection sort” là như vậy, bạn phải chọn và sắp xếp các lá bài theo đúng trình tự của nó. 

Tìm vị trí của phần tử nhỏ nhất trong phân khúc

Tuy nhiên, khi triển khai thuật toán, chúng ta cần phải xác định rằng code của chúng ta không “nhìn” thấy được mà chúng ta phải thực hiện bước so sánh lần lượt, rồi tìm ra giá trị nhỏ nhất và đưa nó về đúng vị trí cần xếp.

Ví dụ như ta có mảng bao gồm các giá trị quân bài [13, K, 8, 5, 9, 2] thì việc đầu tiên là tìm lá bài nhỏ nhất trong mảng, tức là số 2, vị trí của nó ban đầu là 5 (ghi chú: mặc định là theo index đầu tiên là 0).

Selection sort sẽ hoán đổi vị trí số 5 với vị trí số 0, cụ thể [2, 13, K, 8, 5, 9, 2] . Việc tiếp theo của chúng ta là tìm số nhỏ nhất tiếp theo và hoán đổi cho vị trí số 1, và tiếp là vị trí 2, 3, 4.

Triển khai thuật toán

Trong Javascript, có lẽ các bạn cũng không lạ gì hàm sort() , ví dụ:

[ "yellow", "brown", "red", "green"].sort() 
// trả về kết quả ["brown", "green", "red", "yellow"]

Bạn có thể sử dụng hàm có sẵn mà không cần phải đắn đo gì nhiều về cách nó hoạt động, nhưng để nắm bắt được cơ bản về khoa học máy tính, thì thuật toán sắp xếp chọn là bước khởi đầu truyền thống. Vì vậy, bạn cứ coi như là ngôn ngữ không có hàm sort() nào cả.

Chúng ta thử triển khai nó bằng vòng lặp for như sau:

• Lặp toàn bộ mảng, đặt vị trí tạm thời của giá trị nhỏ nhất là vị trí đầu tiên.
• Vòng lặp con thu hẹp mảng lại để so sánh và tìm vị trí giá trị nhỏ nhất tiếp theo trong mảng. Nếu gặp giá trị nhỏ hơn, ta sẽ “đánh dấu” vị trí (index) này.
• Trên vòng lặp tổng, ta so sánh vị trí “đánh dấu” với vị trí giá trị ban đầu, nếu nó khác nhau thì ta “lật” nó ra đằng trước.
• Đối với thuật toán khi chạy và so sánh lần lượt các giá trị bằng vòng lặp con thì vòng lặp lớn đã sắp xếp nó và trả về kết quả theo vị trí mong muốn.

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    // find the smallest index
    let minIndex = i;

    for (let j = i + 1; j < arr.length; j++) {
      if (arr[minIndex] > arr[j]) {
        minIndex = j;
      }
    }

    // swap the index
    if (minIndex !== i) {
      var temp = arr[i];
      arr[i] = arr[minIndex];
      arr[minIndex] = temp;

      // use ES6 destruction array to swap
      // [arr[i], arr[minIndex]]=[arr[minIndex], arr[i]]
    }
  }

  return arr;
}


const arr = [45, 58, 11, 25, 34, 32, 97, 58];

selectionSort(arr)

Đo lường hiệu suất

Thuật toán selection sort thực hiện vòng lặp trên array n , và trên mỗi vị trí, nó phải gọi 1 vòng lặp phụ để xác định vị trí đó có phải là số nhỏ nhất hay không, nếu đúng thì nó sẽ hoán đổi vị trí, do đó thời gian chạy của nó gồm có 3 phần.

Thời gian của số lần chạy của vòng lặp chính trên toàn bộ mảng

Thời gian của số lần chạy của vòng lặp trên toàn bộ mảng là để kiểm tra và gia tăng giá trị biến của vòng lặp mảng con nhằm thu hẹp kích thước của mảng con để gọi hàm tìm vị trí giá trị nhỏ nhất rồi đảo ngược, vì vậy nó mất một hằng số nhất định cho một lần lặp, dùng tiệm cận thì ta cũng có thể xác định thời gian chạy của nó là θ(n).

Thời gian của số lần chạy trên mảng con để tìm vị trí giá trị nhỏ nhất (minIndex)

Sau mỗi lần lặp, mảng được thu hẹp dần lại thành n-1, n-2, n-3... cho đến khi bằng không, vậy cộng tổng thời gian lại là 1+2+3+...+(n-1)+n, là một chuỗi số. Tổng của số đầu và cuối là n+1, và vì nó có tất cả n giá trị nên nó sẽ có n/2 cặp (n chẵn hoặc lẻ), do đó ta có thể rút gọn chuỗi số là (n+1)*(n/2) = n²/2 + n/2. Như ta đã biết, big-θ bỏ qua giá trị hằng số cũng như những giá trị gia tăng nhỏ hơn mà chỉ giữ lại hệ số lớn nhất, tóm lại ta có thời gian chạy để tìm kiếm vị trí giá trị nhỏ nhất là Θ(​n²).

Thời gian của số lần chạy để đảo vị trí

Với thời gian chạy để đảo thứ tự, thì nhìn vào vòng lặp bạn có thể hình dung là với mảng kích thước n thì nó có thể chạy n lần, mỗi lần chạy mất một khoảng thời gian nhất định, vậy ta cũng có thể xác định thời gian chạy của đảo vị trí là θ(n).

Vậy tổng kết lại, ta có tổng số thời gian chạy của toàn bộ thuật toán bao gồm θ(n) cho vòng lặp trên toàn mảng, θ(n) thời gian chạy để đảo vị trí, Θ(​n²) thời gian chạy để tìm vị trí giá trị nhỏ nhất, trong đó Θ(​n²) là giá trị có ý nghĩa ảnh hưởng nhất, vì vậy ta coi Θ(​n²) là thời gian chạy của thuật toán selection sort.

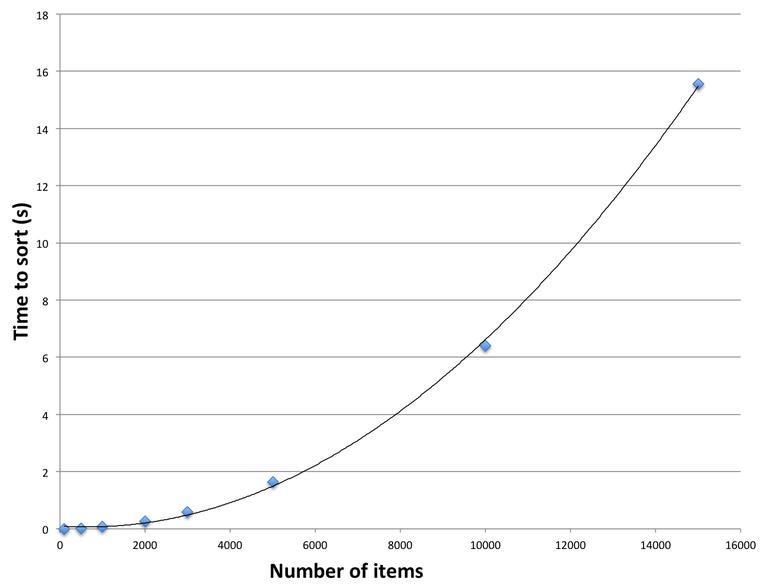
Đồ thị mô tả tiến trình thời gian thực hiện thuật toán