Độ phức tạp của thuật toán

Có rất nhiều người, kể cả tôi và bạn, có thể lập trình được rất nhiều ứng dụng phần mềm khác nhau mà không cần quan tâm đến Khoa học máy tính, tuy nhiên những gì mà chúng ta đang dùng đều là nền tảng của nó, chúng ta đã và đang thừa hưởng thành quả của những người đi trước, do đó nếu nắm bắt được cơ sở, bạn có thể hiểu được nền tảng mà bạn đang ứng dụng là gì, từ đó có thể vận dụng và viết code của mình một cách tốt hơn. Ở phần đầu này, các bạn sẽ tìm hiểu qua về các khái niệm khi phân tích độ phức tạp của thuật toán, tạm nôm na là hiệu suất của hàm bạn viết ra, bạn có thể đo đạc được khả năng thực thi của nó bằng một phương thức nhất định.

Khái niệm về tiệm cận

Khi chúng ta thực hiện một thuật toán nào đó thì điều quan trọng mà ta hay hướng tới đó là thời gian thực thi của thuật toán đó.

Thời gian chạy của của một thuật toán phụ thuộc vào việc máy tính mất bao lâu để chạy những dòng lệnh của thuật toán. Trong số các yếu tố thì sự phụ thuộc phần lớn là dựa vào tốc độ của máy tính, ngôn ngữ lập trình, và cả trình biên dịch để dịch sang mã máy để máy tính có thể chạy được.

Xem xét thời gian chạy của một thuật toán một cách kỹ lưỡng hơn, chúng ta sẽ thấy được 2 ý:

1. Ta phải xác định được thời gian để thực hiện thuật toán dựa trên kích cỡ của input (đầu vào). Do đó, ta có thể coi thời gian thực hiện thuật toán như là một hàm xử lý kích cỡ input của nó.
2. Ta phải chú trọng vào tốc độ tăng trưởng của hàm khi gia tăng kích cỡ input. Ta gọi đây là tỉ suất tăng trưởng của thời gian thực thi.

Để cho dễ hình dung, ta cần đơn giản hóa hàm để phân tích được những phần quan trọng và bỏ qua những phần ít quan trọng hơn. Ví dụ, có một thuật toán 6n² + 100n + 300 đang chạy với kích thước dữ liệu là n .

Khi n đủ lớn, thì 6n² trở thành cụm tăng trưởng lớn nhất so với cụm còn lại. Dưới đây là biểu đồ biểu diễn độ tăng trưởng của dữ liệu đầu vào với giá trị n tăng từ 0 đến 100.

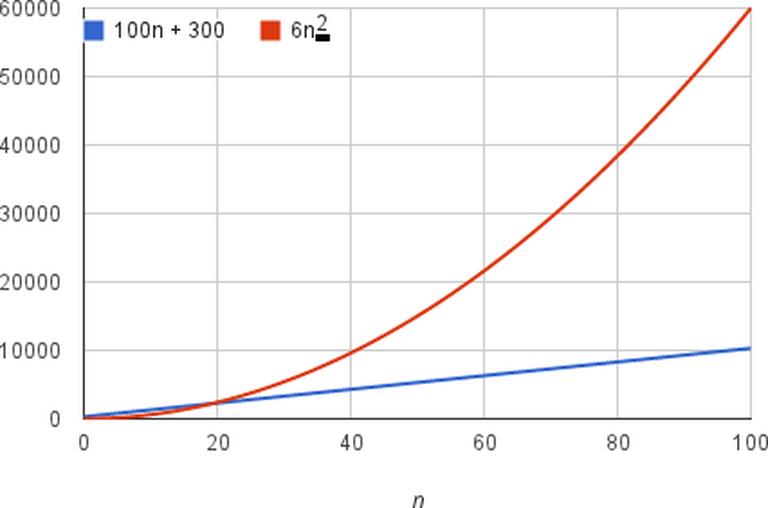
Thời gian chạy của thuật toán này là n² , loại trừ hệ số 6 và cụm 100n +300

Bằng cách loại bỏ cụm ít có ý nghĩa và hệ số hằng số, ta có thể tập trung vào phần quan trọng của thời gian xử lý thuật toán — tỷ lệ tăng trưởng — mà không phải sa lầy vào các chi tiết làm hại não. Khi loại bỏ những yếu tố đó, thì ta có thể gọi đó là tiệm cận. Với tiệm cận thì có 3 dạng sau: tiệm cận big-Θ (Theta) , tiệm cận big-O , và tiệm cận big-Ω (Omega) .

Big-θ (Theta)

Tôi sẽ giới thiệu với các bạn về linear search (tìm kiếm tuyến tính) ở phần sau, tuy nhiên tạm lấy ví dụ ở đâu bằng một hàm linear search đơn giản sau đây:

const linearSearch = (value, inputArray) => {
  for (let i = 0; i < inputArray.length; ++i) {
    if (value === inputArray[i]) {
     return i
    }
  }
  return null
}
    
const Arr = [10, 14, 26, 27, 31, 33, 35, 42, 44]
    
console.log(linearSearch(33, Arr))

Đặt kích cỡ của mảng (array.length) là n . Số lần tối đa của vòng lặp for có thể chạy là n và trường hợp xấu nhất (worse case) xảy ra khi giá trị cần tìm lại không có trong mảng.

Tại mỗi lần lặp, hàm phải thực hiện vài thao tác sau:

• So sánh guess với array.length
• So sánh array[guess] với targetValue
• Trả về giá trị guess nếu tìm thấy
• Tăng lần guess .

Mỗi một lần tính toán như vậy sẽ mất một khoảng thời gian hằng số cho mỗi lần thực thi. Nếu vòng lặp for lặp n lần, thì thời gian cho tất cả n lần lặp sẽ là x₁.n (tổng số lần tính toán cho một lần lặp). Giá trị của x₁.n phụ thuộc vào tốc độ của máy tính, ngôn ngữ sử dụng, trình biên dịch hay thông dịch thành ngôn ngữ máy tính và nhiều yếu tố khác nữa.

Để thiết lập vòng lặp for bao gồm lần khởi đầu là 0 và có thể trả về null ở cuối thì nó mất một khoản chi phí nhỏ, ta gọi thời gian cho chi phí này là hằng số x₂ . Vì vậy thời gian tổng của linear search đối với trường hợp xấu nhất là x₁.n + x₂

Như đã bàn ở trên, thì x₁ và x₂ không ảnh hưởng đến tỷ lệ tăng trưởng của thời gian thực thi, mà điều quan trọng là thời gian chạy cho trường hợp xấu nhất trong linear search ở mảng có kích thước n . Kí hiệu mà ta gọi cho thời gian chạy này là Θ(n), đọc là Theta theo tiếng Hy lạp, và hay được gọi là big-Theta.

Khi cho một thời gian chạy cụ thể là Θ(n), lúc n đủ lớn, thời gian chạy ít nhất là k₁.n và thời gian chạy nhiều nhất là k₂.n với k₁ , k₂ là hằng số . Xem biểu đồ dưới đây:

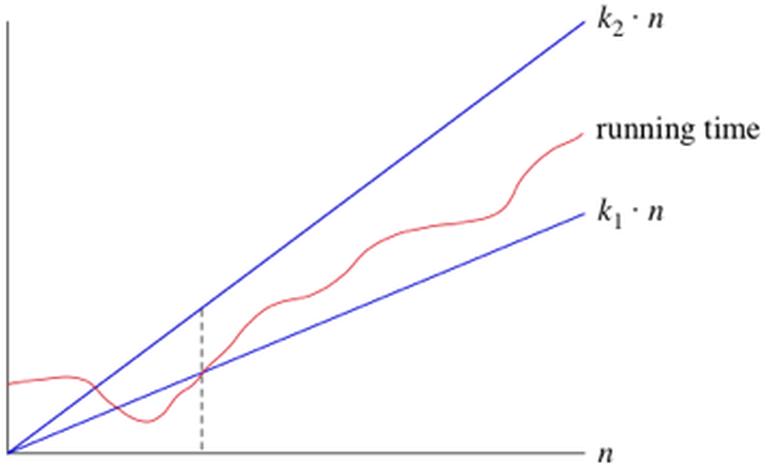
Big-O

Ở trên ta sử dụng ký hiệu big-Θ cho cận trên và dưới bằng các hằng số khác nhau, tuy nhiên đôi khi chúng ta chỉ cần quan tâm đến cận trên. Ví dụ, mặc dù thời gian chạy trong trường hợp xấu nhất của binary search (tìm kiếm nhị phân) là Θ(log₂​n), sorry các bạn, số 2 nhỏ nhưng Medium không hiểu :( , nhưng nếu nói thời gian chạy của binary search trong mọi trường hợp là Θ(log₂​n) thì không đúng. Điều gì xảy ra nếu tìm thấy kết quả ở lần tìm đầu tiên? Tức là nó chạy trong Θ(1), thời gian chạy của binary search không bao giờ xấu hơn Θ(log₂​n) hoặc chỉ có thể tốt hơn.

Vì vậy big-O là một ký hiệu tiệm cận để chỉ ra là “thời gian chạy tăng nhiều lắm cũng có nhiêu đây nhưng nó cũng có thể tăng chậm hơn”.

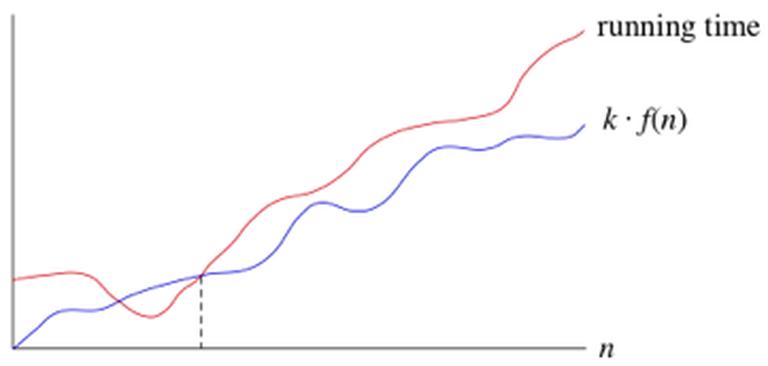
Nếu một thời gian chạy là O(f(n)), và n đủ lớn, với một hằng số k nào đó thì thời gian chạy nhiều nhất là k.f(n) . Dưới đây là biểu đồ biểu diễn một thời gian chạy O(f(n))

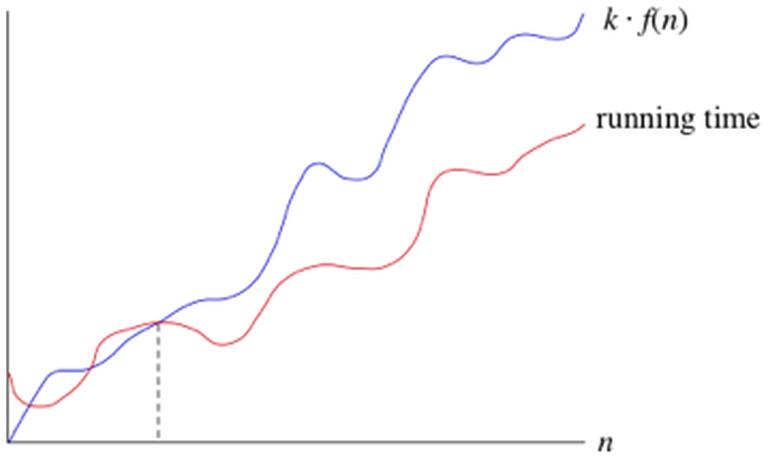
Chúng ta sử dụng ký hiệu big-O cho tiệm cận trên khi thời gian chạy gia tăng nhiều nhất với một kích cỡ input đủ lớn.

Vậy là ta đã có khái niệm để mô tả cho binary search một cách khái quát nhất cho mọi trường hợp, tức là thời gian chạy của binary search luôn là O(log₂​n), và kể cả khi tính đến thời gian chạy xấu nhất là Θ(log₂​n) thì O(log₂​n) vẫn bao quát được.

Nhìn lại ký hiệu big-Θ thì ta cũng có thể thấy được big-O bản chất nó cũng là big-Θ khi xét ở một khía cạnh nhất định, chỉ khác là big-Θ bao gồm cả cận trên và cận dưới. Ví dụ, trường hợp xấu của binary search là Θ(log₂​n) thì cũng là O(log₂​n). Tuy nhiên, nếu xét ngược lại thì không phải lúc nào cũng đúng, chẳng hạn như binary search lúc nào cũng chạy trong O(log₂​n) thời gian nhưng không phải lúc nào cũng chạy trong Θ(log₂​n) thời gian.

Vì big-O chỉ xác định ở tiệm cận trên và nó không là một khái niệm tiệm cận chặt chẽ, nên thoạt nhìn có vẻ nó không đúng, nhưng xét về mặt kỹ thuật, nó đúng. Ví dụ, thuật toán binary search chạy trong O(​n) thời gian là hoàn toàn đúng, vì thời gian chạy không thể tăng nhanh hơn một hằng số n lần, thậm chí còn chậm hơn.

Lấy ví dự như sau, giả sử như bạn có 100K trong túi và nói với thằng bạn “Tao có tiền, nhưng mà không nhiều hơn 10 triệu đâu” , tức là việc khai báo của bạn hoàn toàn đúng dù nó quá khập khiễng với con số mà bạn đang so sánh. Số 10 triệu là cận trên của 100K, cũng giống O(​n) thời gian chạy của binary search, dù nó có lớn tới mức là O(​n²), O(​n³), O(​2ⁿ). Nhưng không phải trường hợp nào cũng đúng với Θ(​n²), Θ(​n³), Θ(​2ⁿ).

Big-Ω

Trong một vài trường hợp, nếu như ta chỉ muốn biết số lượng thời gian ít nhất mà thuật toán thực hiện mà không cần quan tâm đến cận trên của nó, ta dùng ký hiệu big-Ω, theo tiếng Hy Lạp gọi là “Omega”.

Khi nói đến ký hiệu big-Ω nghĩa là tính tiệm cận dưới khi thời gian chạy gia tăng ít nhất với một input đủ lớn.

Chúng ta cũng biết Θ(f(n)) cũng bao gồm O(f(n)), thì nó cũng bao gồm Ω(f(n)). Nên ta có thể nói trường hợp xấu nhất của thời gian chạy cho thuật toán binary search là Ω(log₂​n).

Tương tự như ví dụ về số tiền ở trên, bạn có 10 triệu, nhưng lại nói với thằng bạn của bạn là “Trong túi tao có ít nhất 100K”, điều này đúng nhưng cũng là sự cường điệu. Vì vậy, ta cũng có thể nói trường hợp xấu nhất của Ω(1), bởi rõ ràng nó lấy hằng số thời gian thấp nhất.

Kết luận

Mặc dù khi tính toán độ phức tạp của thuật toán, ta đều cố gắng càng chính xác càng tốt. Tuy nhiên, các bạn cũng đã nắm được phần nào các khái niệm về big-Θ, big-O, big-Ω, và đây phương pháp tính toán độ phức tạp của thuật toán. Thông thường các bạn sẽ nghe nhiều đến big-O khi nhắc đến việc phân tích một thuật toán nào đó, lý do vì sao thì các bạn cũng có thể nắm được sau khi xem các ví dụ ở trên.

Hy vọng qua nội dung này các bạn có thể nắm được khái quát về cách tính độ phức tạp về thời gian xử lý của một thuật toán, nếu bài viết có chỗ nào thiếu sót, hoặc giải thích còn khó hiểu, các bạn có thể góp ý cho tôi.

Nội dung tham khảo từ khóa học Khoa học máy tính trên Khan Academy